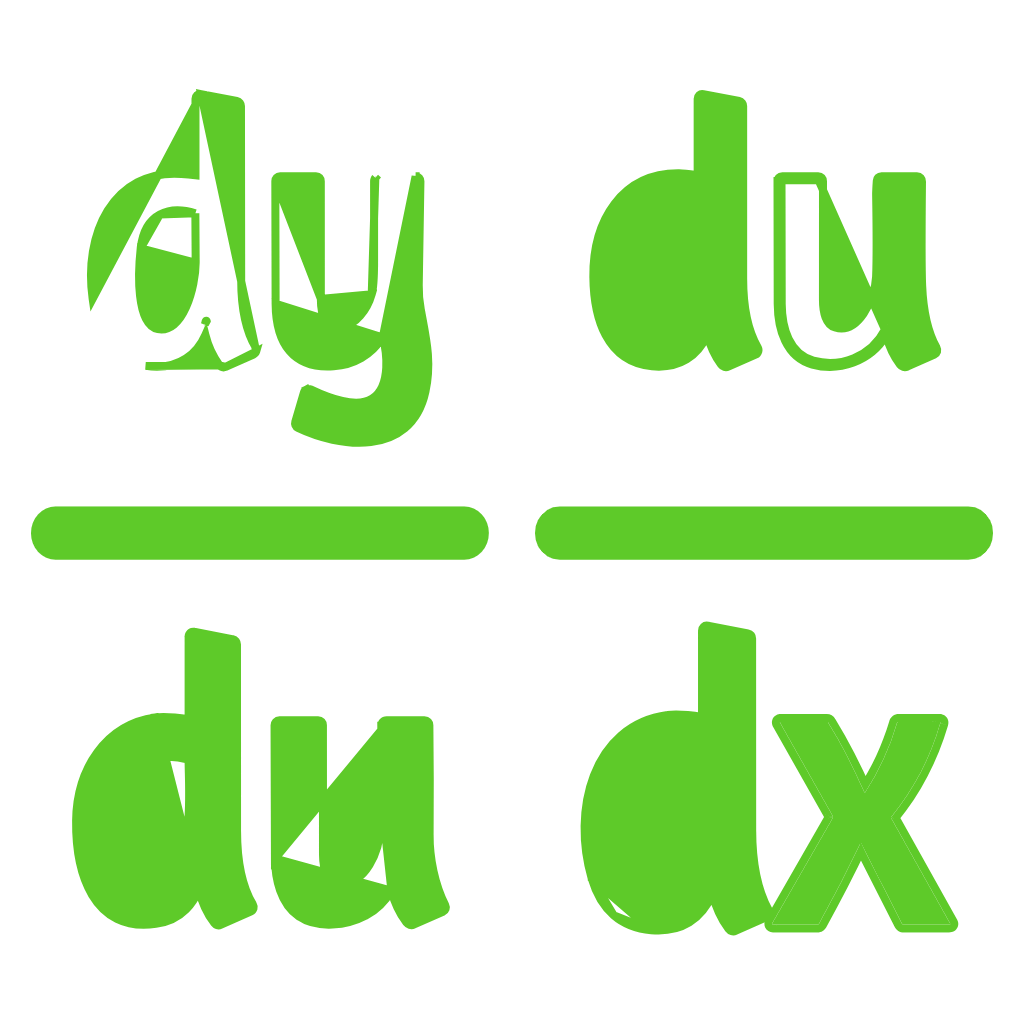Introduction to Inverse Derivative Calculator
The derivative of inverse function calculator is the best online tool that is designed to find the rate of change of an inverse function. It is used to determine the complicated inverse derivation function in the simplest form.

Doing the calculation of complex inverse differentiation is more confusing because of the function's complex nature. That is why, we introduce our derivative of the inverse calculator to solve an inverse function derivative in just one click.
This calculator specializes in finding the derivative of inverse functions. It is designed to handle the computation of derivatives for functions that are expressed in terms of their inverses. The Inverse Derivative Calculator simplifies the process of computing these derivatives, providing accurate results efficiently.
Our Calculator is suitable for scenarios involving inverse functions, whereas our derivative at point calculator is ideal for determining derivatives at specific points along a function.
What is the Inverse Function?
An inverse function is defined as a function that reverses the original function. In calculus inverse function differentiation is a technique that is used to solve inverse functions.
Additionally, By utilizing the derivative graph calculator in conjunction with the concept of inverse functions, you can gain deeper insights into the relationship between functions and their derivatives, enhancing their understanding of calculus concepts.
Formula used by Derivative of Inverse Function Calculator
The inverse derivative function formula is based on numerator and denominator form. The formula used by the inverse derivative calculator is given,
$$ \frac{d}{dx} x \;=\; 1 \;=\; \frac{d}{dx} f (f^{-1} (x)) \;=\; f’ (f^{-1} (x)) . f^{-1} ‘ (x) $$
So,
$$ \frac{d}{dx} f^{-1} (x) \;=\; \frac{1}{f’(f^{-1}(x))} $$
Here, where f^-1 shows inverse function of f(x) = 1/f(x)
f`(x) shows derivation of the function along the x-axis
This formula is based on the relationship between a function and its inverse. It allows for the determination of the derivative of the inverse function using the derivative of the original function.
How does the Derivative of the Inverse Calculator Work?
The derivative inverse calculator works according to the principle of derivative rules. These derivative rules are used in the calculator whenever you enter any inverse function as input because these formulas are already installed in its software.
When you give an inverse function as an input in the derivative of inverse functions calculator, it analyzes the function. After recognizing f(x) and g(x) as the numerator and denominator respectively, it applies the derivative formula of the quotient rule for inverse functions.
Instantly, It will give you a solution of the derivative function along with a graph of the given function for better understanding. for further exploration and a comprehensive understanding of derivatives, you can use our derivative definition calculator. This calculator offers insights into the fundamental definition of derivatives, fostering a deeper understanding of calculus principles and their applications.
Now let's examine an example of an inverse differential function using our inverse derivative calculator.
Example of Inverse Derivative
An example of the inverse derivative problem to understand how to solve it manually is given,
Example:
Use the inverse function theorem to find the derivative of
$$ g(x) = \sqrt[3]{x} $$
Solution:
The above function is the inverse of the function f(x) = x3. As g’(x) = 1/f’(g(x)) begin by finding f’(x). So,
$$ f’(x) \;=\; 3x^2 $$
$$ f’(g(x)) \;=\; 3( \sqrt[3]{x})^2 \;=\; 3x^\frac{2}{3} $$
Finally,
$$ g’(x) \;=\; \frac{1}{3x^\frac{2}{3}} $$
We will rewrite the equation as a power of x to get,
$$ g(x) \;=\; x^\frac{1}{3} $$
Now differentiate using the power rule to obtain,
$$ g’(x) \;=\; \frac{1}{3} x^\frac{-2}{3} \;=\; \frac{1}{3x^\frac{2}{3}} $$
Thus it is the final solution of our function with specific limits. Additionally, Ffor a deeper understanding of the slope of curves and to calculate the slope at a specific point, you can go through our slope of the curve calculator. Our caluclator provides an easy method to calculate the slope of a tangent line of the curve.
How to Use an Inverse Derivative Calculator?
The derivative of inverse function calculator provides an easy procedure for the calculation of an inverse function in a few simple steps. The following steps will help you to find the solution of inverse derivation problems.
- Enter your inverse function at the input field
- Choose the variable which you want to evaluate derivation
- Review your function before hitting on calculate button
- Click on the “Calculate” button to get the solution of your given function
Related: For handling complex functions and exploring alternative methods of differentiation, you can go through our derivative of log calculator. This tool simplifies the process of finding derivatives using logarithmic differentiation, providing solutions for enhanced understanding and analysis.
Outcome Obtained from Derivative Inverse Calculator
You will get the solution of the inverse differential problem after you enter the inverse problem as an input in this derivative of the inverse calculator. It will give some extra steps along with the result of the inverse derivative function. It may contain as:
- Result section will give you the solution of the inverse function
- Possible steps section will give you a detailed solution of the inverse problem
- Plot option will provide a graph of the given function
- Recalculate button enables a user to do more evaluation for practice.
For further exploration and to delve into more advanced calculus techniques, you can utilize our implicit derivative at a point calculator. This calculator provides step-by-step solutions for implicit differentiation problems, aiding in understanding and mastering this concept.
Reason to Choose our Derivative of Inverse Functions Calculator
The inverse derivative calculator is designed and developed in such a way that it calculates complicated inverse functions into simplest calculations. It is the most trustworthy tool because it gives an exact solution every time you enter any type of inverse function.
The inverse function is sometimes difficult to calculate the derivative problems when you do manual calculations. It would be best for you to use our calculator, which allows users to solve any type of inverse function in a few seconds.
Our derivative of inverse function calculator will help you to learn the derivative of the inverse function easily, especially for students who are not familiar with derivative rules.
In addition to its primary function, our calculator offers comprehensive functionality. For instance, you can explore advanced calculus techniques, such as calculating the second derivative of implicit functions, using our second derivative implicit differentiation calculator.
Advantages of Using our Tool
This derivative of the inverse calculator provides numerous benefits when you use it for calculation. It is a simple device to use because you just need to follow some simple steps to get the solution of an inverse differentiation function.
- It is a free tool available online, so you do not pay for any premium fee.
- You can use this device for learning and practicing with different examples.
- The derivative inverse calculator saves your time on doing long-term calculations of derivatives, as it helps you to learn more in less time.
- Our inverse derivative calculator provides you with accurate solutions according to differential rules.
- It provides a user-friendly interface so that anyone can easily access to calculate inverse differential functions in no time.
Related: For access to this calculator and many more useful tools, visit our All Calculator page.